Solution to Challenge #1

Ok, let’s start with a naive approach. We shall implement a Least Recently Used cache using Python’s builtin Dict.

class LRUCache:
    def __init__(self, capacity: int):
        self.capacity = capacity
        self.cache = {}
        self.order = []

    def get(self, key: int) -> int:
        if key in self.cache:
            # Move the accessed key to the end to mark it as recently used
            self.order.remove(key)
            self.order.append(key)
            return self.cache[key]
        return -1

    def put(self, key: int, value: int) -> None:
        if key in self.cache:
            # Update the value and move the key to the end
            self.cache[key] = value
            self.order.remove(key)
            self.order.append(key)
        else:
            if len(self.cache) >= self.capacity:
                # Evict the least recently used item
                lru_key = self.order.pop(0)
                del self.cache[lru_key]
            # Insert the new key-value pair
            self.cache[key] = value
            self.order.append(key)

# Example usage:
cache = LRUCache(2)  # Capacity of 2

cache.put(1, 1)
cache.put(2, 2)
print(cache.get(1))  # Returns 1
cache.put(3, 3)      # Evicts key 2
print(cache.get(2))  # Returns -1 (not found)

Works perfectly fine. The trouble? This implementation isn’t strictly O(1). Clue: Can you identify parts which aren’t O(1) in the above code? They’re actually O(n).

self.order.remove(key) # in put method if key is found in cache

This involves searching for the `key` in `self.order`.

The other line is,

self.order.pop(0) # in put method if key isn't there in the cache

Removing the first element of a list requires shifting all subsequent elements one position to the left, which is again O(n).

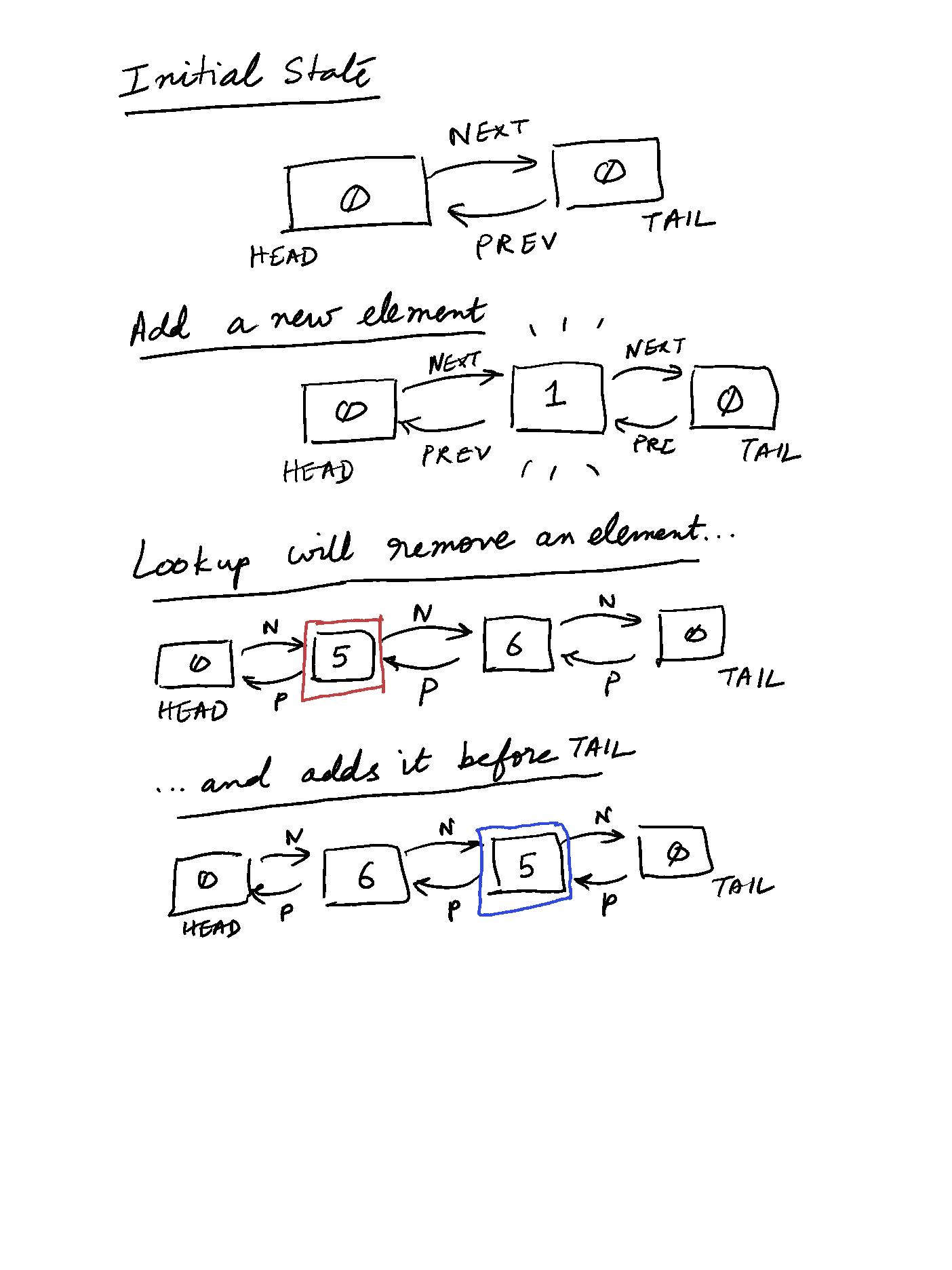
Our second attempt at solving the problem involves a Dict and a doubly linked list(DLL). The Doubly linked list will maintain the order of usage, while the Dict will provide O(1) access.

class Node:
    def __init__(self, key, value):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None

class LRUCache:
    def __init__(self, capacity: int):
        self.capacity = capacity
        self.cache = {}
        self.head = Node(0, 0)
        self.tail = Node(0, 0)
        self.head.next = self.tail
        self.tail.prev = self.head

    def _remove(self, node: Node):
        prev_node = node.prev
        next_node = node.next
        prev_node.next = next_node
        next_node.prev = prev_node

    def _add(self, node: Node):
        prev_node = self.tail.prev
        prev_node.next = node
        node.prev = prev_node
        node.next = self.tail
        self.tail.prev = node

    def get(self, key: int) -> int:
        if key in self.cache:
            node = self.cache[key]
            self._remove(node)
            self._add(node)
            return node.value
        return -1

    def put(self, key: int, value: int) -> None:
        if key in self.cache:
            self._remove(self.cache[key])
        node = Node(key, value)
        self._add(node)
        self.cache[key] = node
        if len(self.cache) > self.capacity:
            lru = self.head.next
            self._remove(lru)
            del self.cache[lru.key]

# Example usage:
cache = LRUCache(2)  # Capacity of 2

cache.put(1, 1)
cache.put(2, 2)
print(cache.get(1))  # Returns 1
cache.put(3, 3)      # Evicts key 2
print(cache.get(2))  # Returns -1 (not found)
cache.put(4, 4)      # Evicts key 1
print(cache.get(1))  # Returns -1 (not found)
print(cache.get(3))  # Returns 3
print(cache.get(4))  # Returns 4

• __init__: Initializes the cache with a given capacity, a dictionary for fast access, and a dummy head and tail for the doubly linked list.

• _remove: Removes a node from the doubly linked list.

• _add: Adds a node right before the tail (most recently used position).

• get: Retrieves a value from the cache and moves the accessed node to the most recently used position.

• put: Inserts a new key-value pair, moves it to the most recently used position, and evicts the least recently used item if the capacity is exceeded.

Here’s a simple illustration of how the DLL will work.

Now, try implementing the following error/constraint handling strategies:

1. Cache capacity must be a positive integer

2. Keys and values must only be of a certain type. Ex: Key must be an integer, value must be a string.

3. Some utility functions in the cache, like is_empty, which returns a boolean stating whether the cache is empty. Override __len__ which returns the length of the cache. A clear method, which clears all the items in the cache.

Happy coding!